최대실체조건(MMC/MMS) 공차
정의와 위치도공차 적용
기계공학, 항공공학을 전공하는 학생들이 2,3학년 전공수업 시간에 공차 개념을 다루면서 처음 접하게 되는 MMC/LMC 의 개념에 대해 자세히 알아보겠습니다.
처음에는 이 개념이 쉽게 와닿지 않기 때문에 정확하게 개념을 정리해두는 것이 좋습니다.
최대 실체조건 MMC(Maximum Material Condition) 정의
형체의 실체, 즉 부품의 부피가 최대인 상태, 조건입니다.
부품의 부피가 최대가 된 상태(조립 시 가장 불리한 조건)를 기준으로 기하공차를 적용하는 개념입니다.
MMC를 처음 사용하게 된 시기는?
2차 세계대전이 끝나고 미국에서 항공산업 분야에 적용하기 시작한 새로운 공차 개념으로, 파트 간 상호 공차를 활용하여 파트 간 제작 호환성을 매우 높여준 방식입니다.
현재까지도 널리 사용되고 있습니다.
최대 실체조건 MMC 사용 범위
1. 결합되는 형체에 적용 (구멍<->핀 등)
2. 결합되는 부품 간의 상호 의존성을 고려하여 치수의 여분을 추가 공차로 적용
3. 중심 또는 중간면이 있는 치수공차를 가지는 형체에 적용
아마 위의 내용이 와닿지 않을 텐데요,
아래에서 그림과 같이 자세히 설명 드릴것이니 크게 걱정하지 않으셔도 되겠습니다.
최대 실체치수 MMS (Maximum Material Size)
형체가 최대실체일 때의 치수.
축, 외측 형체 : 최대 허용치수 = 최대 실체치수(MMS)
구멍, 내측 형체 : 최소 허용치수 = 최대 실체치수(MMS)
반대되는 개념으로는 LMC/LMS가 있습니다.
최소 실체조건 LMC(Least Material Condition)
최소 실체치수 LMS (Least Material Size)
형체의 실체, 즉 부품의 부피가 최소인 상태와 치수.
그럼 어떻게 MMC를 적용하는 지, 기호 적용사례를 간단히 확인하겠습니다.
규제 형체에 MMC를 적용하는 경우
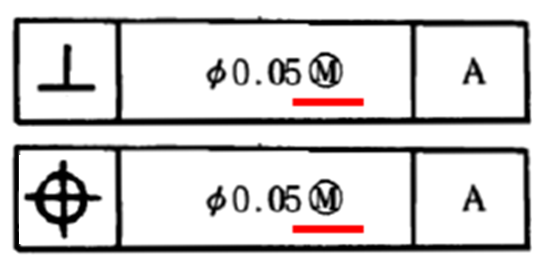
공차값(숫자) 뒤에 MMC 기호를 기입합니다.
MMC는 일반적으로 직각도/위치도 공차에 많이 사용됩니다.
데이텀 형체에 MMC를 적용하는 경우

데이텀 문자(Ex. A B C) 뒤에 MMC 기호를 기입합니다.
이번 포스팅에서는 위치도 공차 MMC 적용 사례에 대해 설명드리겠습니다.
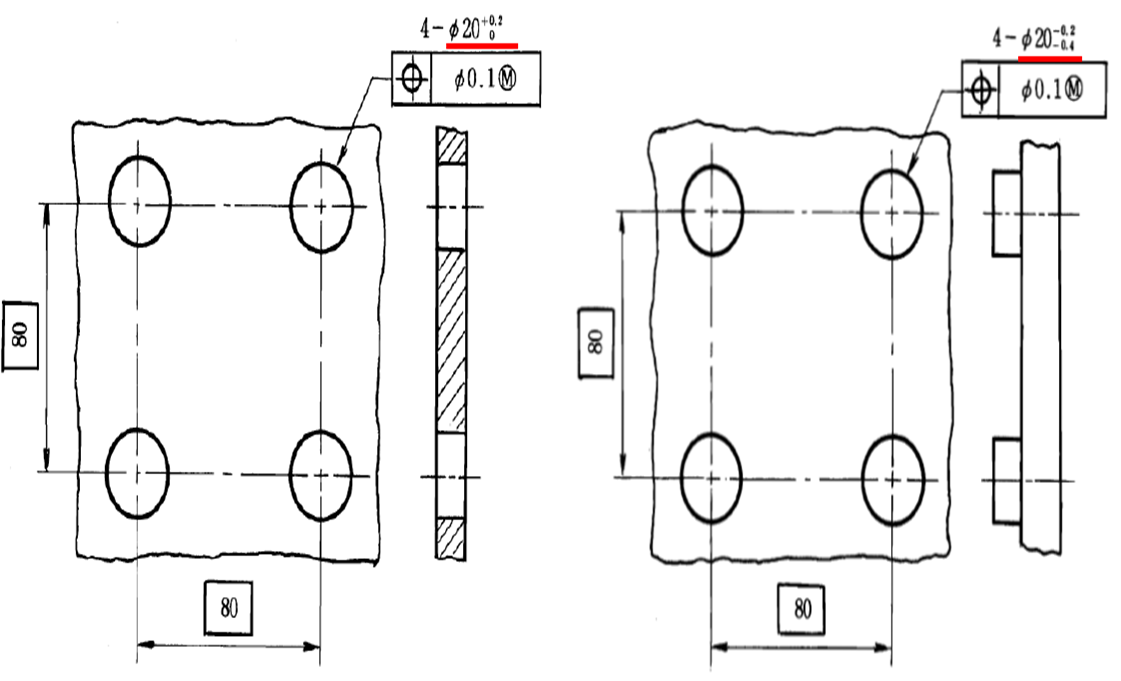
위 그림에서
[왼쪽] 구멍이 있는 파트
[오른쪽] 구멍에 맞는 핀을 가진 파트
2개 간의 공차관계로 설명하겠습니다.
먼저, hole이 4개 있는 파트의 경우,
공차를 적용하면 hole의 크기는 20.0~20.2 입니다.
hole의 지름이 가장 작을 때 == 파트의 부피 최대 == MMC = 20.0
이며, pin의 크기는 공차 적용 시 19.6~19.8 에서
pin의 지름이 가장 클 때 == 파트의 부피 최대 == MMC = 19.8
이 됩니다.
그럼 이 때, hole(20.0) 과 pin(19.8) 간에 0.2의 공차가 발생하는데요,
이 공차를 각각 0.1씩 나누어 가지면서, MMC 조건일 때 사용합니다.
MMC(최대실체조건) / MMS(최대실체치수)를 제대로 이해하기 위해서는
VC(실효조건) / VS(실효치수)를 반드시 알고 가야 합니다.
실효 조건 VC (Virtual Condition)
대상 형체의 최대실제치수와 기하공차의 결합 효과에 의한 한계 상태
실효 치수 VS(Virtual Size)
결합되는 상대 부품과의 가장 빡빡하게 결합되는 조건의 치수
결합되는 상대 부품의 최대 실체치수
실효 치수일 때, 기하공차 = 0
축(or 핀)의 실효치수
= 축(or 핀)에 결합되는 파트 구멍의 최대실체치수(MMS)
구멍(or 홈)의 실효치수
= 구멍(or 홈)의 최대실체치수(MMS) (-) 해당 기하공차
= 구멍(or 홈)에 결합되는 파트 핀의 최대실체치수(MMS)

![[MMC/MMS]최대실체조건 공차 정의와 위치도 적용](https://blog.kakaocdn.net/dna/JgPuh/btrCVOWsLz5/AAAAAAAAAAAAAAAAAAAAABEiAF1DNoH1IZOmi5fy6B8rjgrOd12gFdMFa2kqhRLx/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=vkK5Ijei0qoEwHiG94PJLZluzWI%3D)
실효치수(VS)는 결합되는 상대 부품과의 가장 빡빡하게 결합되는 조건의 치수인데요,
이 말은
가장 불리한 조건에서도 상대 파트와 조립이 가능해야 한다
는 것을 의미합니다.
왜 그렇게 되는 것인지, 아래 그림에서 확인할 수 있습니다.
1. 구멍의 최대실체조건(MMC, 파트의 부피 최대)
= hole size 20.0 일 때
위에서도 언급했지만, hole size 가 20.0~20.2 의 조건에서
hole size가 작아야 파트의 부피가 최대가 됩니다.
따라서 20.0 일 때 파트의 최대실체치수(MMS) 조건이 성립합니다.
![[MMC/MMS]최대실체조건 공차 정의와 위치도 적용](https://blog.kakaocdn.net/dna/euB1Fi/btrCZSQ4Ciq/AAAAAAAAAAAAAAAAAAAAAEY28cr9sw7zQefK1LfAe0fBAKG1KhpsI44dnF8XN-sk/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=NpiFGr3Ylwpw7GGh18uoIlG1sqo%3D)
MMC 조건 하에서 위치도 공차가 Ø 0.1
이기 때문에
지름 0.1 내에서 자유롭게 hole center를 이동할 수 있습니다.
![[MMC/MMS]최대실체조건 공차 정의와 위치도 적용](https://blog.kakaocdn.net/dna/8GD9O/btrCYvWj8X2/AAAAAAAAAAAAAAAAAAAAANicp6n0evaVKkPgl5jV7kNyFQGQfRMvXc14EdOlpTKd/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=%2B5kGpx6tUcy4PYwp6VkInrc1Pvo%3D)
따라서 hole center가 공차 내에서 가장 아래/위로 갈 때,
Ø20.0의 hole은 위와 같이 파트에 뚫리게 되며,
![[MMC/MMS]최대실체조건 공차 정의와 위치도 적용](https://blog.kakaocdn.net/dna/xsN7r/btrCZRECoZc/AAAAAAAAAAAAAAAAAAAAAN2tGxqYq0-Z4pP3PjVbd6oeTkicCiVsCs5oCsZuHyx5/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=im11yxUzXmA%2BAMThav3SM8E2Z3s%3D)
hole center가 공차 내에서 가장 오른쪽/왼쪽으로 갈 때,
위와 같은 hole이 만들어집니다.
2. 구멍의 최소실체조건(LMC, 파트의 부피 최소)
= hole size 20.2 일 때
반대로 hole size가 20.2로 가장 클 때, 파트의 부피는 최소가 됩니다.
![[MMC/MMS]최대실체조건 공차 정의와 위치도 적용](https://blog.kakaocdn.net/dna/ypMod/btrCY7t97ax/AAAAAAAAAAAAAAAAAAAAAM8s88CYt-blPz8Kkza9rtz_gp71UqIwRHcOIz_IE-eo/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=ZOOdGFnUiW2FYxcS0%2BTZnOGsYHw%3D)
자세히 보여드리기 위해서 그림에서
19.9와 0.3 의 치수 비율을 무시하고 0.3을 크게 보이도록 그렸습니다.
Hole size가 20.2 가 되더라도,
실효치수(VS)인 19.9의 원이 20.2 원에 내접하는 것을 볼 수 있습니다.
MMC/LMC 내용을 정리해 보면,
최대실체치수(MMS) 20.0의 hole을 공차 내에 어디로 이동하던지 간에,
최소실체치수(LMS) 20.2의 hole을 공차 내에 어디로 이동하던지 간에,
Ø19.9의 실효치수(VS) 원에 내접하게 됩니다.
공식을 적용해보면,

*내측형체, 적용되는 기하공차
= 제작된 치수 - MMC + 주어진 기하공차
Ex 1) Ø20.0 hole 제작 [MMC]
= 20.0 - 20.0(MMC) + 0.1 = 0.1 (tolerance, 공차)
Ex 2) Ø20.1 hole 제작
= 20.1 - 20.0(MMC) + 0.1 = 0.2 (tolerance, 공차)
Ex 3) Ø20.2 hole 제작 [LMC]
= 20.2 - 20.0(MMC) + 0.1 = 0.3 (tolerance, 공차)
이 되는 것을 알 수 있습니다.
이해가 한 번에 잘 안 될 수 있으니, 천천히 그림을 보면서 이해하시는 것이 좋고,
직접 그려서 치수를 대보고 익히는 방법 또한 좋습니다.
3. 핀의 최대실체조건(MMC, 파트의 부피 최대)
= pin size 19.8 일 때

핀의 사이즈는 19.6~19.8 이기 때문에, 돌출된 형태를 가지고 있는 핀은,
지름이 가장 큰 19.8에서 최대실체치수(MMS)를 가지게 됩니다.
![[MMC/MMS]최대실체조건 공차 정의와 위치도 적용](https://blog.kakaocdn.net/dna/oAti7/btrCXlmmGAZ/AAAAAAAAAAAAAAAAAAAAABaWdKYmvu2mJY0Uf-VcHJ6OQ43hYqOXWPKxUdGLhX_y/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=E8rDYo6su8U8YZqkhvNF4eMk6Zk%3D)
MMC 조건 하에서 공차가 Ø0.1 이기 때문에,
위치도 공차 Ø0.1 내에서 hole의 중심이 이동 가능한 것을 볼 수 있습니다.
![[MMC/MMS]최대실체조건 공차 정의와 위치도 적용](https://blog.kakaocdn.net/dna/bYD2R6/btrCW1V0lsc/AAAAAAAAAAAAAAAAAAAAABsSc0Yy7prp3J5fC85koNkzC7W9TVz8kV1LKyB6OD36/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=9mSGo4i7Heotnxf0k4cKSkCisSo%3D)
그리고 공차 내에서 이동한 19.8의 원이
결국 하늘색의 실효치수(VS) Ø19.9 내에 모두 내접하는 것을 알 수 있습니다.
4. 핀의 최소실체조건(LMC, 파트의 부피 최소) = pin size 19.6 일 때
이번에는 hole size가 가장 작은, Ø19.6 최소실체치수(LMS)의 경우를 보겠습니다.
![[MMC/MMS]최대실체조건 공차 정의와 위치도 적용](https://blog.kakaocdn.net/dna/OufA1/btrCVQGLvWK/AAAAAAAAAAAAAAAAAAAAANhcYDchV4UzO2Japn3BMixy4TXSsFsPY4RC7OYVuUza/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=vbyhMaSov4Ow6HaFPdjDjEDIy5A%3D)
자세히 보여드리기 위해서 그림에서
19.6과 0.3 의 치수 비율을 무시하고 0.3을 크게 보이도록 그렸습니다.
지름이 19.8에서 19.6으로 줄어들면서,
기존 공차 0.1에 0.2를 더해서 0.3만큼 hole center를 이동할 수 있게 되었습니다.
![[MMC/MMS]최대실체조건 공차 정의와 위치도 적용](https://blog.kakaocdn.net/dna/ryvTJ/btrCZSjgcJ3/AAAAAAAAAAAAAAAAAAAAAGJeqrLqLmR3L8XjxDNI8iHE-V52Q0Rocvi6lrShmDt1/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=cgGnlWcX9sw470Qs0aCKS8JdAc0%3D)
마찬가지로 hole center를 어디로 가져가든지,
실효치수(VS) Ø19.9에 내접하는 것을 확인할 수 있습니다.
LMC/MMC를 정리해보면,
최대실체치수(MMS) 19.8의 pin을 공차 내에 어디로 이동하던지 간에,
최소실체치수(LMS) 19.6의 pin을 공차 내에 어디로 이동하던지 간에,
Ø19.9의 실효치수 원에 외접하게 됩니다.
공식을 적용해보면,

*외측형체 적용되는 기하공차
= MMC - 제작된 치수 + 주어진 기하공차
Ex 1) Ø19.8 pin 제작 [MMC]
= 19.8(MMC) - 19.8 + 0.1 = 0.1 (tolerance, 공차)
Ex 2) Ø19.7 pin 제작
= 19.8(MMC) - 19.7 + 0.1 = 0.2 (tolerance, 공차)
Ex 3) Ø19.6 pin 제작 [LMC]
= 19.8(MMC) - 19.6 + 0.1 = 0.3 (tolerance, 공차)

결과적으로 실효치수(VS)가 같은
두개의 파트([구멍(hole) <--> 핀(pin)] 는최악의 조건 하에서도 조립이 가능합니다.
[항공/항공산업의 역사] - 보잉 비행기(항공기/민항기), 엔진 개수 & 복도 개수(광동체/협동체)
[항공/항공산업의 역사] - 항공기(비행기) 쌍발기(엔진 2개) 시대와 3개/4개 항공기 쇠퇴이유 분석
[항공/항공산업의 역사] - 보잉 비행기(항공기/민항기), 7-7 Numbering(B7X7) 이유와 예외(B720) 분석
세계에서 가장 큰 여객기, A380 가장 많이 구매한 항공사 순위 BEST 14
2022년 5월 현재 항공사에서 여전히 운영하고 있는 가장 큰 민간여객기는 단연 에어버스(AIRBUS)사의 A380-800 입니다. 와... 저 비행기 뭐야? 왜 저렇게 커? 공항에서 초대형 여객기 A380과 중소형 크기
airviewkorea.com
미국 보잉 항공기 예약 "5천대 돌파".. 항공사가 가장 많이 구매한 기종 TOP 6
전세계 대부분 항공사들이 운영하는 100인승 이상의 비행기 시장은 미국의 보잉(BOEING)사와 유럽의 에어버스(AIRBUS)사가 80% 이상 차지하고 있습니다. 보잉사가 역사가 더 오래된 만큼, 어떤 기준으
airviewkorea.com
"비행기 1대에 수천억!?" 아시아나항공 제일 비싼 항공기 TOP 6
대형항공사 큰 비행기는 1대 가격이 얼마나 해? 보통 저가항공사들이 사용하는 200석 내외의 중소형 보잉/에어버스 비행기는 1대에 약 1000억 정도입니다. 신형 새 비행기는 좀 더 비싸고, 중고 구
airviewkorea.com
"20시간 날아간다고?" 가장 먼 거리 비행하는 초장거리 항공 노선 TOP 10
진짜 한 번 비행에 20시간 날아갈 수 있어? 기술이 많이 발전하면서 한 번에 20시간 이상 비행도 가능한 시대가 되었습니다. 물론 아직은 일반적인 조건에서 다 가능한 것은 아니고, 좌석을 일반
airviewkorea.com
"승무원 월급, 연봉 반토막.." 정부 휴업 지원금도 더 적게 받는 이유는?
항공사 직원들, 정부에서 월급 지원 받는 거 아니야? 2020년 3월, 코로나로 인해 국제선이 거의 다 중단되면서 항공사, 여행사, 면세점 등 큰 타격을 입은 업종들은 정부에서 "특별고용지원 대상"
airviewkorea.com
'항공공학 > 항공기 도면 해석' 카테고리의 다른 글
| 항공기 도면 방위/방향 : Looking Forward(FWD)/After(AFT) 및 6가지 종류 (0) | 2019.04.21 |
|---|---|
| 항공기의 방위/방향/좌표 위치표시방법 : FS/BL/WL (0) | 2019.04.18 |







